2 분 소요

Information Theory

  • entropy
    • unpredictability of information content
      • it captures the value of surprises
      • information from independent events is “additive”
      • information is non-negative

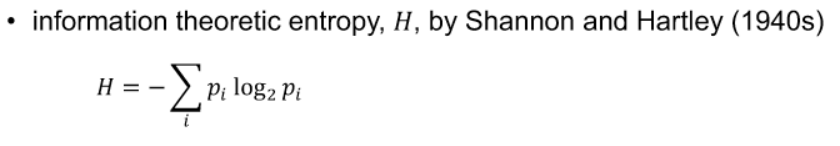
    • as distributions become more uniform, entropy goes up.
    • Gaussian distribution has the maximum entropy among possible distributions on an infinite range with a finite mean and variance

    Entropy is a measure of uncertainty or disorder in a set of outcomes or information. In information theory, three related concepts are often used: marginal entropy, joint entropy, and conditional entropy.

    1. Marginal Entropy:
      • Definition: Marginal entropy quantifies the uncertainty associated with a single random variable in isolation, without considering any other variables.
      • Formula: For a discrete random variable \((X)\), the marginal entropy \((H(X))\) is calculated as \((H(X) = -\sum_{x} P(x) \log_2(P(x)))\), where \((P(x))\) is the probability of each possible outcome of \((X)\).
      • Interpretation: A higher marginal entropy indicates greater uncertainty or randomness associated with the individual variable.
    2. Joint Entropy:
      • Definition: Joint entropy measures the uncertainty associated with a pair of random variables considered together.
      • Formula: For two discrete random variables \((X)\) and \((Y)\), the joint entropy \((H(X, Y))\) is calculated as \((H(X, Y) = -\sum_{x, y} P(x, y) \log_2(P(x, y)))\), where \((P(x, y))\) is the joint probability of the outcomes \(((x, y))\).
      • Interpretation: Joint entropy provides a measure of uncertainty when considering the combined outcomes of two variables.
    3. Conditional Entropy:
      • Definition: Conditional entropy quantifies the remaining uncertainty in one random variable given the knowledge of another.
      • Formula: For two discrete random variables \((X)\) and \((Y)\), the conditional entropy \((H(X \mid Y))\) is calculated as \((H(X \mid Y) = -\sum_{x, y} P(x, y) \log_2\left(\frac{P(x, y)}{P(y)}\right))\), where \((P(x, y))\) is the joint probability, (P(y)) is the marginal probability of (Y), and the sum is taken over all possible outcomes of \((X)\) and \((Y)\).
      • Interpretation: Conditional entropy reflects the remaining uncertainty in \((X)\) when \((Y)\) is known. A lower conditional entropy indicates that knowledge of \((Y)\) reduces the uncertainty about \((X)\).

    In summary, marginal entropy captures the uncertainty of individual variables, joint entropy quantifies the uncertainty of multiple variables considered together, and conditional entropy measures the remaining uncertainty in one variable given the knowledge of another. These concepts are fundamental in understanding and analyzing the information content and relationships between random variables in various domains, including information theory, statistics, and machine learning.

  • mutual information
    • measures how much information is shared
    • the more independent they are, the smaller MI is
  • Cross Entropy
  • causality - information flow

  • transfer entropy

태그:

카테고리:

업데이트:

참고